2013-2014 год. 4-й тур (очный), Франция (28 августа 2014)
Условия задач
Содержание:
- Каляки-маляки
- Подходящие годы
- Рыцари и лжецы
- Трещины
- Оладушки
- Грузчик
- Квадратики
- Тетраэдр
- Числа и фигуры
- Много прямых
- Соревнование
- Дон и Магдалина
- Взвешивания
- Крот
- Счастливое число
- Магический брильянт
- Консервные банки
- Белое и чёрное
1. Каляки-маляки
Коля закалякал четыре цифры равенства, в котором каждая цифра от 0 до 9 встречалась ровно по одному разу. Восстановите закаляканные цифры.
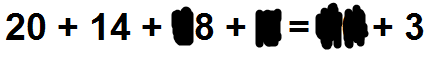
2. Подходящие годы
Инопланетяне-математики хотели высадиться на Землю в 2014 году, поскольку они посчитали, что (20-14)+1 равно 2+0+1+4 (легко проверить, что выражения равны 7). Инопланетяне вообще считают подходящим для высадки любой год из четырёх цифр такой что:
- разделив номер года на две части и получив таким образом два двузначных числа,
- вычислив разность этих двузначных чисел (то есть, вычтя из большего числа меньшее, независимо от того, какое из них стоит справа, а какое слева),
- и прибавив к разности один, мы получим ответ, равный сумме цифр года. Инопланетяне нашли три подходящих года для высадки на Землю: 2114 год (так как 21-14+1 = 2+1+1+4), 2214 год (так как 22-14+1 = 2+2+1+4), и 2314 год (так как 23-14+1 = 2+3+1+4). Каков следующий после 2314 подходящий год?
3. Рыцари и лжецы
На далёком острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда врут. Робинзон встретил шестерых островитян и спросил у них, правильной ли дорогой он идёт к столице острова. Первые трое ответили на его вопрос “да” или “нет”. После чего четвёртый островитянин сказал: “Ровно один из троих, ответивших до меня, солгал”. Пятый островитянин заявил: “Ровно двое из четверых, говоривших до меня, солгали”. Наконец, шестой подытожил: “Ровно трое из пятерых, говоривших до меня, солгали”. Известно, что ровно один из трёх островитян, говоривших последними, рыцарь. Кто же именно рыцарь из трёх островитян?
4. Трещины
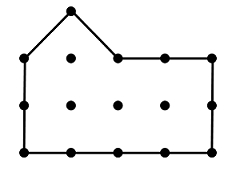
На рисунке изображён фасад дома. Леночка вбила гвоздик в одну из чёрных точек, но тут от гвоздика по стене побежали три трещины, разделив фасад на три одинаковые части. Каждая трещина представляет из себя ломаную линию, отрезки которой соединяют две соседние точки по вертикали, горизонтали, или диагонали. Нарисуйте трещины.
5. Оладушки
Братец иванушка испёк четыре оладцшка разных размеров и положил их на блюде как показано на левой картинке. Прежде чем нести оладьи на стол, сестрица Алёнушка хочет разложить их по порядку, от самого большого снизу до самого маленького сверху, как показано на правой картинке. Для этого у сестрицы Алёнушки есть деревянная лопатка. Она засовывает свою лопатку под один из оладьев (кроме самоговерхнего) и переворачивает целиком всю стопку из двух, трёх или четырёх оладий на лопатке. За какое наименьшее число переворотов Алёнушка может разложить оладушки по порядку?

Конец категории CE.
6. Грузчик
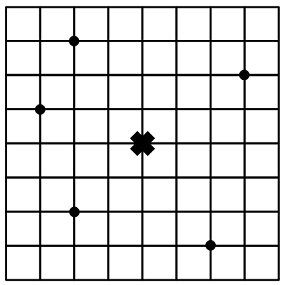
В пяти вершинах решётки, отмеченных чёрными точками, стоят одинаковые сундуки. Грузчик должен собрать все сундуки в одном узле решётки; при этом он может передвигаться только по линиям решётки (по вертикали или по горизонтали). Например, чтобы собрать все сундуки в точке, отмеченной крестиком, грузчику в сумме придётся пройти с сундуками на плечах расстояние в 23 клетки. Грузчик спросил приятеля математика, в каком узле решётки ему следует собрать сундуки, чтобы в сумме ему пришлось пройти как можно меньшее расстояние с сундуками на плечах. Математик нашёл нужный узел решётки и грузчик собрал там все сундуки, неся их по самому которкому пути вдоль линий решётки. Сколько клеток ему пришлось пройти с сундуками на плечах?
7. Квадратики
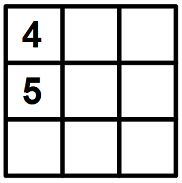
В клетках квадрата 3Х3 были написаны все числа от 1 до 9 (по одному числу в каждой клетке). При этом сумма четырёх чисел во всех четырёх квадратах 2Х2 была, во-первых, одной и той же и, во-вторых, максимальной возможной с учётом первого условия. Семь из девяти чисел стёрли. Восстановите их.
8. Тетраэдр
На рисунке изображён тетраэдр (пунктиром показано заднее ребро). В вершинах тетраэдра (в окружностях) и на его рёбрах (в квадратиках) стоят числа от 1 до 11, причём каждое встречаются ровно по одному разу, кроме одного числа, которое вообще не используется. Известно, что число, стоящее на ребре, всегда на один больше суммы чисел, стоящих в вершинах на его концах. Например, вершины с числами 1 и 4 должны быть соединены ребром с числом 6. Кроме того, числа в вершинах a, b, c, d идут в возрастающем порядке. Расставьте числа в вершины и рёбра, согласно условиям.
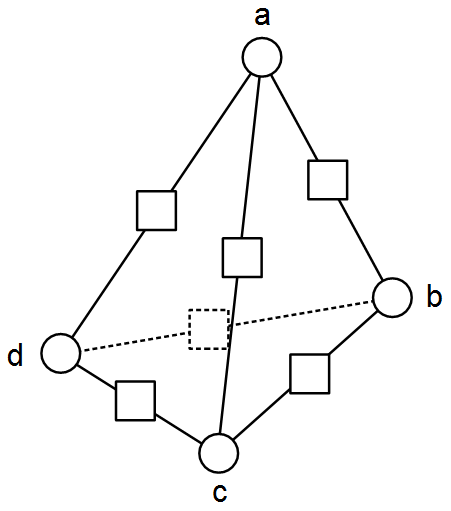
Конец категории CM.
9. Числа и фигуры
Каждая маленькая фигура на рисунке обозначает действительное неотрицательное число строго меньшее единицы. Каждая средняя фигура обозначает натуральное число, равное сумме маленькой и средней фигуры той же формы. Например, если сложить числа, обозначенные маленьким и средним квадратом, то получится число, обозначенное большим квадратом. Какие числа обозначают большие фигуры?
10. Много прямых
На плоскости проведено несколько прямых, первые три из которых обозначены D_1, D_2 и D_3. Известно, что прямая D_1 пересекает ровно 20 других прямых, а прямая D_2 - ровно 14 других прямых. Какое наименьшее количество прямых может пересекать прямая D_3?
11. Соревнование
Аня, Боря и Валя устроили соревнование по головоломкам. Первому, решившему головоломку, присуждается a очков, второму - b очков, а третьему - c очков, где a > b > c > 0 - некоторые целые числа, одинаковые для всех головоломок в соревновании. В сумме по всем головоломкам Аня получила 20 очков, Боря - 14 очков, а Валя - 11 очков. Кроме того, известно, что Боря первым решил головоломку Судоку. Сколько очков он получил за головоломку Какуро?
Конец категории C1.
12. Дон и Магдалина
Острова A, B и C находятся в вершинах равностороннего треугольника. Корабль Дон отправляется с острова A к острову B и далее плывёт вдоль сторон треугольника с постоянной скоростью против часовой стрелки. Корабль Магдалина отправляется с острова B к острову A и далее плывёт вдоль сторон треугольника с постоянной скоростью по часовой стрелке. Скорости кораблей не равны друг другу. В первый раз корабли встречаются в точке I, между A и B, в 20 морских милях от A. Во второй раз корабли встречаются в точке J, между B и C. Третий раз корабли встречаются в точке K, между C и A, в 14 морских милях от A. На рисунке отношение между длинами отрезков не соблюдены. Найдите периметр треугольника ABC в морских милях. Ответ округлите до ближайшего целого числа.
13. Взвешивания
Имеется шесть гирек занумерованных от 1 до 6 в порядке возрастания их масс; то есть, вторая гирька весит больше первой, третья больше второй и так далее. Массы всех гирек различны. Имеются также весы с двумя чашами. За одно взвешивание разрешается положить по три гирьки на каждую чашу весов. Известно, что имеется способ разложить гирьки так, что весы окажутся в равновесии. Требуется добиться равновесия не больше чем за три взвешивания. Какие две гирьки следует положить на одну чашу весов с гирькой номер 1 во время первого взвешивания? Укажите их номера в возрастающем порядке.
14. Крот
На рисунке изображён вертикальный срез подземного домика, в котором живёт крот. Крот любит каждый день добираться от входа в домик (буква T на рисунке) к своей спальне (буква C на рисунке) по новому пути. При этом, путь не дожен проходить два раза по одному и тому же туннелю или по одному и тому же перекрёстку. Кроме того, по тунелям со стрелками разрешается передвигаться только в направлении стрелок. Крот посчитал, что всего у него в запасе 2014 разных путей. Сколько из них проходят через левый нижний угол (вопросительный знак на рисунке)?
15. Счастливое число
Натуральное число называется счастливым, если у него ровно в 13 раз меньше положительных делителей, чем у его куба. (При подсчёте делителей учитываются 1 и само число. Так, у числа 30 ровно 8 положительных делителей, что в 8 раз меньше, чем у его куба 30^3=27000). Сколько положительных делителей может быть у счастливого числа?
16. Магический брильянт
В кругах на рисунке расставлены целые числа от 0 до 14, причём все числа встречаются по одному разу, кроме трёх, которые вовсе не используются. Во всех девяти отрезках из трёх или четырёх дисков сумма чисел одна и та же, причём наименьшая возможная. Числа в кругах a, b, c идут в возрастающем порядке. Расставьте числа в круги.
Конец категорий L1, GP.
17. Консервные банки
Имеется набор одинаковых консервных банок в форме цилиндра, причём диаметр цилиндра в два раза больше его высоты. При пересылке консервные банки складываются в кубические коробки так, чтобы хотя бы одна сторона каждой банки (то есть основание цилиндра) полностью прилегала к грани коробки. На левой картинке показана самая маленькая коробка, в которую можно поместить три банки. На правой картинке показана самая маленькая коробка, в которую можно поместить шесть банок. Оказалось, что сторона куба на правой картинке ровно на миллиметр больше стороны куба на левой картинке. Найдите диаметр консервной банки в миллиметрах. Ответ округлите до ближайшего миллиметра. Вам может потребоваться приближение \sqrt{65}\approx 8,062.
18. Белое и чёрное
Клетки прямоугольника 4Х3 можно раскрасить в чёрный и белый цвет 4096 способами. Мастер выпускает игры, в которых у чёрно-белого прямоугольника 4Х3 можно целиком переставить две строки или два столбца. Две игры называются эквивалентными, если раскраску одной из них можно превратить в раскраску другой такими перестановками. Например, на рисунке показаны четыре эквивалентные игры. Какое максимальное количество попарно неэквивалентных игр удастся сделать мастеру?
Конец категорий L2, HC.
