Универсальный алгоритм для компьютерных логических игр

24.01.2014 - Alexey Nurgaliev

В статье рассмотрены способы создания универсальной компьютерной программы, играющей в логические игры («Крестики-нолики», «Реверси» и т.п.). Также проведен анализ некоторых универсальных алгоритмов выбора оптимального хода.

Программа должна состоять из двух частей: алгоритма выбора оптимального хода для игрока-компьютера и набора функций, определяющих правила игры (рассматриваться будут только антагонистические игры).

Антагонистическая игра (или игра с нулевой суммой) - некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

Рассмотрим каждую часть отдельно.

1. Алгоритм выбора оптимального хода

Алгоритм должен быть универсальным (не зависеть от правил игры) и обеспечивать хороший уровень игры. Первый рассматриваемый алгоритм, удовлетворяющий этим условиям – алгоритм минимаксного дерева.

Игрок в текущей позиции пытается сделать все возможные ходы и максимизировать свой выигрыш, а также минимизировать выигрыш другого игрока. Перебор позиций проводится при помощи поиска в глубину (depth-first search, DFS) до достижения некоторой заданной глубины \(d\) или конца игры.

Обозначим:

\(p\) – текущая позиция;
\(p_i\) – все позиции, доступные из позиции \(p\);
\(F(p)\) – выигрыш игрока в позиции \(p\).

Если позиция p является терминальной, то для нее определена функция \(f(p)\), определяющая выигрыш игрока, которому принадлежит ход в этой позиции.

Позиция называется терминальной, если из нее нет разрешенных ходов (достигнуты конец игры или необходимая глубина перебора).

Выигрыш игрока будет равен:

\[F(p) = f(p),\]

если позиция \(p\) – терминальная, иначе

\[F(p) = max(-F(p_i))\]

Достоинства:

Простая реализация.
Гарантированно будут рассмотрены все ходы.

Недостаток: требуется проверять все возможные ходы и при увеличении глубины перебора количество рассматриваемых позиций растет экспоненциально.

Количество перебираемых вариантов можно уменьшить, если прекращать поиск точной оценки хода, когда стало известно, что этот ход не может стать лучше, чем один из ходов, рассмотренных ранее[1].

Алгоритм альфа-бета отсечений при вычислении оценки позиции иcпользует верхнюю и нижнюю допустимые границы.

Обозначим:

alpha – верхняя граница;
beta – нижняя граница;
\(F_{ab}(p,alpha,beta)\) – функция, вычисляющая оценку позиции \(p\) методом альфа-бета отсечений.

Функция Fab должна удовлетворять условиям:

\(F_{ab}(p,alpha,beta) \le alpha\), если \(F(p) \le alpha\)
\(F_{ab}(p,alpha,beta) = F(p)\), если \(alpha < F(p) < beta\)
\(F_{ab}(p,alpha,beta) \ge beta\), если \(F(p) \ge beta\)

Достоинства:

В большинстве случаев значительно уменьшается количество рассматриваемых позиций при переборе.
Реализация легко получается из реализации алгоритма мини-максного дерева.
Результат не хуже, чем при полном переборе позиций.

Недостаток: сложность алгоритма остается такой же, как и при полном переборе позиций (экспоненциальной). Существуют случаи, когда выигрыш от оптимизации незначителен или отсутствует.

Сравнение количества перебранных позиций для первых 10 ходов в игре «Реверси» на поле 8х8 при использовании алгоритмов минимаксного дерева и альфа-бета отсечений (глубина перебора 6 позиций, программа играет против человека, человек делает ход первым)

Номер хода	Минимаксное дерево поиска (полный перебор)	Перебор с использованием альфа-бета отсечений
1	16 251	1 015
2	61 730	1 712
3	568 484	10 948
4	1 083 976	14 325
5	1 624 623	13 598
6	2 412 356	18 287
7	1 847 605	15 328
8	5 389 480	30 807
9	4 870 334	22 508
10	3 390 729	21 994

Альтернативой алгоритму минимаксного дерева является использование метода Монте-Карло.

Метод Монте-Карло - общее название группы численных методов, основанных на получении большого числа реализаций случайного процесса, вероятностные характеристики которого совпадают с аналогичными величинами решаемой задачи.

В нашей задаче (поиск оптимального хода): для текущей позиции \(p\) выбираются все возможные позиции \(p_i\) и с каждой из этих позиций разыгрывается большое количество случайных партий. Позиция, для которой соотношение побед и поражений будет наилучшим, выбирается для следующего хода.

Достоинства:

Высокий уровень игры при большом количестве разыгрываемых случайных партий.
Хорошо поддается распараллеливанию.
Линейная сложность.

Недостатки:

Хорошие ходы могут не попасть в случайную выборку.
Для сильной игры требуется производительный компьютер.

Например, одна из сильнейших программ для игры в го, «MoGo», использующая этот метод, запускалась на компьютере производительностью 15 Терафлопс[3] (для сравнения, производительность процессора Intel Core i7-975 0.06 Терафлопс[2], а производительность суперкомпьютера СКИФ МГУ 47,17 Терафлопс[4]).

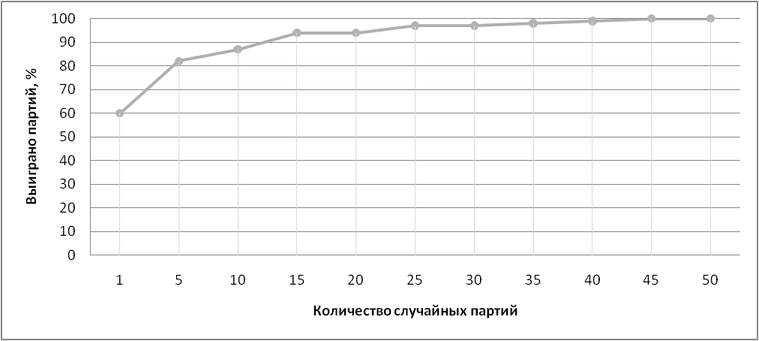
График зависимости количества выигранных партий в игру «Реверси» на поле 8х8 для программы, использующей метод Монте-Карло с разным числом разыгрываемых случайных партий, играющей против программы, использующей алгоритм альфа-бета отсечений с глубиной перебора 6 позиций.

2. Способы описания правил.

В программе алгоритм получает сведения о правилах игры через вызов специальных функций. Пример набора функций, достаточного для большинства логических игр:

Задание начальных условий.
Проверка возможности хода.
Выполнение хода и оценка позиции.
Проверка условия конца игры.

Для обеспечения универсальности, функции должны поддерживать выбор правил для разных игр. Правила могут быть представлены разными способами.

1. Набор функций для каждой игры описывается вместе с остальными функциями (алгоритмом выбора хода и т.п.) и компилируется в один исполняемый файл.

Достоинства:

Простая реализация.
Высокая скорость работы игровых функций.

Недостатки:

Для добавления правил игры необходимы весь исходный код программы и компилятор.
Необходимо знание языка программирования, на котором написана программа.

2. Подключение набора функций в виде внешнего модуля (например, DLL).

Большинство шахматных программ подключается к шахматным оболочкам в виде внешних модулей (для взаимодействия обычно используется специальный протокол UCI - Universal Chess Interface).

Достоинства:

Возможность создания любого количества игр, не изменяя исход-ный код программы.
Высокая скорость работы функций, реализованных в модулях.

Недостатки:

Необходимость знания языка программирования, программу на котором можно скомпилировать в модуль.
Нужен интерфейс для взаимодействия с модулями.

3. Реализация программы как интерпретатора языка программирования. Каждая функция описываются в виде программы, которую можно интерпретировать и которая может получать доступ к игровым переменным. При вызове функции программа интерпретируется с заданными параметрами (номер игрока, координаты хода и т.п.) и, если требуется, возвращает не-которое значение (выигрыш игрока, возможность хода и т.п.).

Достоинства:

Количество возможных игр не ограничено.
Не требует средств разработки и каких-либо компиляторов.
Язык должен быть очень простым и обучение программированию на нем не должно занимать много времени. (В язык могут быть встроены функции, облегчающие какие-либо часто встречающиеся операции (например, функции, подсчитывающие количество идущих подряд клеток определенного цвета).

Недостатки:

Требуется изучение специального языка.
Язык может уступать по функциональности распространенным языкам высокого уровня.
Скорость работы значительно ниже, чем при использовании скомпилированного кода, т.к. тратится дополнительное время на интерпретацию.

Пример программы на интерпретируемом языке, описывающей правила игры “Крестики-нолики” на поле 3х3:

function init #загрузка параметров игры
{
 setHeight({3})   #высота игрового поля
 setWidth({3})    #ширина игрового поля
 setDepth({2})    #глубина перебора позиций
}

function checkMove #проверка правильности хода
{
 if cellEmpty(param0[{1}],param0[{2}]) #проверка, свободна ли клетка
	 return {1}
 return {0} 
}

function makeMove #сделать ход и установить счет игроков (предполагается, что ход возможен)
{
 setCell(param0[{1}],param0[{2}],param0[{0}])
 if equal($win(),param0[{0}])
  setScore(param0[{0}],{1}) #в случае победы, игроку сделавшему ход, начисляется 1
				#очко
}

function endGame #признак конца игры
{	
 if $win() 
  return {1} #игра закаканчивается, если кто-либо выиграл
	
 #также игра заканчивается, если не осталось пустых клеток
 i = {-1}
 while less(i=inc(i),{3})
  if notequal(VNum({0},i),{0})
   return {0}			
 return {1}
}

4. Правила создаются при помощи визуального редактора. Наборы действий для каждой функции могут собираться из большого числа стандартных блоков, которые могут отображаться в удобном для пользователя виде.

Такой подход использует среда разработки Scratch, разработанная в MIT.

Схема из блоков может быть автоматически преобразована в программный код, который может интерпретироваться, либо компилироваться в программный модуль.

Достоинства:

Не требуется специального обучения программированию.
Функции, составленные из блоков, удобно редактировать.

Недостаток: высокая сложность реализации подхода.

Это был краткий обзор универсальных алгоритмов выбора оптимального хода и способов определения правил для логических антагонистических игр.

Файлы на Github

Литература:

An Analysis of Alpha-Beta Pruning [Article] / auth. Knuth D. E. Moore R. W. // Artificial Intelligence. - 1975. - 4 : Vol. 6
Processors - Intel® microprocessor export compliance metrics [Online]. - http://www.intel.com/support/processors/sb/cs-023143.htm
Sensei’s Library: MoGo [Online]. - http://senseis.xmp.net/?MoGo
SKIF MSU [Online] // TOP500 Supercomputing Sites. - http://www.top500.org/system/ranking/9240

Данная статья была опубликована в сборнике “Энергия и талант молодёжи - залог развития наукоёмких производств. Сборник научных трудов XII Областной научно-практической конференции молодых учёных. - Т. 1 - Псков: Издательство ППИ, 2010.