Фракталы

19.01.2014 - Alexey Nurgaliev

В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.

Фрактал – сложная геометрическая фигура, обладающая свойством самоподобия, т.е. из всей фигуры можно выделить части, подобные целой фигуре. Примеры самоподобных множеств известны с XIX века. Термин «фрактал» (от лат. fractus - раздробленный) впервые ввел в 1975 году математик исследовательского центра IBM Бенуа Мандельброт.

Фракталы можно разделить на несколько видов:

Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
Алгебраические фракталы – строятся на основе алгебраических формул.
Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Некоторые примеры алгебраических и геометрических фракталов

Фрактал Мандельброта

Рассмотрим последовательность комплексных чисел:

\[z_{k+1} = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c\]

Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:

прямоугольное окно C с разрешением $m \times n$ точек;
значение $r_{min} = 2$ – минимальный радиус расходимости множества Мандельброта
максимальное число итераций $k_\max$

Если точка $z_k$ вышла за пределы круга радиуса $r_\min$ при $k \lt k_\max$, то процесс вычисления останавливается.

Построение: для каждой точки $c_{ij} \in C (i = \overline{1, n}, j = \overline{1, m}, c_x \in [-2; 1], c_y \in [-2; 1,5])$ запустим итерационный процесс:

\[x_{k+1} = x_k^2 - y_k^2 + c_x, x_0 = c_x\] \[y_{k+1} = 2 x_k y_k + c_y, y_0 = c_y\]

где $k = 0, 1, 2, \dots, k_\max$ и $\sqrt{x_k^2 + y_k^2} \leqslant r_\min$.

Составим матрицу M , элементы которой $m_{ij} \in [1; k_\max]$ равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала $[1, k_\max]$ некоторый цвет.

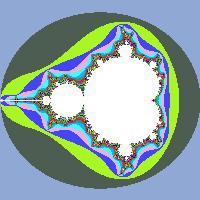
Mandelbrot 1 Mandelbrot 2

Если представить множество в общем виде:

\[z_{k+1} = z_k^N + c\]

то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для $N = 4$ и $N = 7$:

Mandelbrot 3 Mandelbrot 4

Демо на codemore

Фрактал Жюлиа

Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:

\[z_{k+1} = z_k^2 + c, k = 0, 1, 2, \dots\]

Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:

значение c фиксируется: $c = 0,36 + 0,36i$
начальное значение $z_0$ перебирается дискретно в области $C \in [-1;1] + [-1;1]i$

Julia 1

Рассматривая множество в общем виде: $z_{k+1} = z_k^N + c$ и изменяя N и с, можно получать разнообразные фрактальные множества:

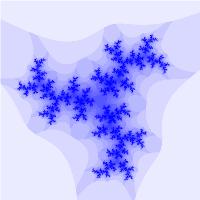
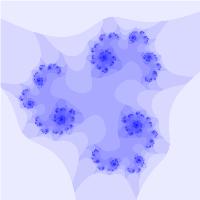
Julia 2 Julia 3 Julia 4

Демо на codemore

Бассейны Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.

Рассмотрим уравнение:

\[p(z) = z^3 - 1\]

Общая формула метода Ньютона имеет вид:

\[z_{k+1} = z_k - \frac{f(z_k)}{f'(z_k)}\]

При выборе различных $z_0$ процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.

Подставив $p(z)$ в формулу метода, получим итерационную формулу для построения фрактала:

\[z_{k+1} = z_k - \frac{z_k^3 - 1}{3z_k^2}\]

Итерационный процесс останавливается при:

\[\left| z_{k+1}^3 \right| \leqslant r_\min\]

Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Newton 1

Если записать формулу в общем виде:

\[p(z) = z^N - 1\] \[\left| z_{k+1}^N - 1 \right| \leqslant r_\min\]

то можно получить изображения фракталов более сложной формы:

Newton 2 Newton 3 Newton 4

Демо на codemore

L-системы

В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).

Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.

L-система определяется как $G = (V, \omega, P)$ , где

V - алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.

Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.

Например, L-система имеет вид:

Переменные: A B

Аксиома: A

Правила: $(A \rightarrow AB) (B \rightarrow BA)$

После нескольких применений правил из аксиомы получаются строки:

0) A

1) AB

2) ABBA

3) ABBABAAB

4) ABBABAABBAABABBA

…

Для построения графической интерпретации L-системы используется «черепашья графика», т.е. символам из V присваиваются команды управления некоторым простым интерпретатором («пройти вперед», «повернуться», и т. д.).

Пример некоторых фракталов, построенных с помощью L-систем - кривая дракона и растение:

LSys Dragon LSys Plant

Демо на codemore

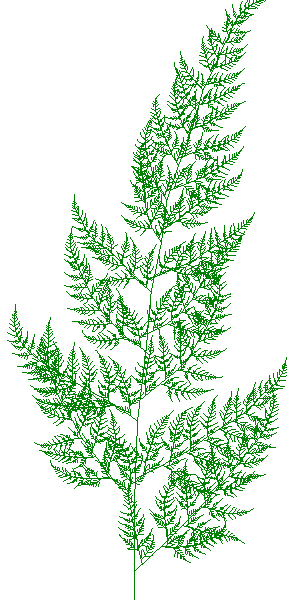
Лист папоротника

Существует несколько способов построения этого фрактала.

1) Построение с помощью системы итерируемых функций (IFS)

Производится 20 итераций функции $f(x, y)$. Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:

Вероятность	$$x'$$	$$y'$$
0,01	$$0$$	$$0,16y$$
0,85	$$0,85x + 0,04y$$	$$-0,04x + 0,85y + 1,6$$
0,07	$$0,20x - 0,26y$$	$$0,23x + 0,22y + 1,6$$
0,07	$$-0,15x + 0,28y$$	$$0,26x + 0,24y + 0,44$$

После выполнения всех итераций точка рисуется на экране.

Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке $[0;1]$.

Fern 1

2) Рекурсивное построение

Для построения используется процедура (псевдокод):

procedure fern(p0,h,ψ,side,δ,rec){
 if (rec=0) or (k2*h&lt; δ) then exit;
 p1=p0+[0,k1*h]*R(ψ)
 p2=p0+[0,k2*h]*R(ψ)
 line(p0,p2) /* процедура построения отрезка по двум точкам */
 fern(p1,m1*h,ψ-side*(φ1+φ0),-side,δ,rec-1)
 fern(p2,m2*h,ψ+side*(φ2+φ0),side,δ,rec-1)
 fern(p2,m3*h,ψ-side*(φ3-φ0),side,δ,rec-1)
}

$R(\phi) = \begin{pmatrix} \cos(\phi) && \sin(\phi) \\ -\sin(\phi) && \cos(\phi) \end{pmatrix}$ - матрица поворота на угол φ.

Параметры процедуры:

$p_0 = [x_0; y_0]$ - координаты начальной точки
h – высота листа
ψ – угол отклонения листа от вертикали
side – направление изгиба ветви
δ – минимальная длина ветви ветвящегося отрезка
rec – максимальная глубина рекурсии

Рекомендуемые значения углов и коэффициентов: $\phi_0 = 14,9^{\circ}, \phi_1 = 37,7^{\circ}, \phi_2 = 36,8^{\circ}, \phi_3 = 17,6^{\circ}, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849$.

Fern 2

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале $(-10^{\circ}; 10^{\circ})$, можно получить изображения:

Fern 3 Fern 4

Демо на codemore

Литература:

Никулин Е. А. Компьютерная геометрия и алгоритмы машинной графики. – СПб.: БХВ-Петербург, 2005
“L-System”:http://en.wikipedia.org/wiki/L-system
“Фрактал”:http://ru.wikipedia.org/wiki/Фрактал
“Лист папоротника”:http://algolist.manual.ru/graphics/fern.php
“Синтез фракталов: IFS и L-системы”:http://habrahabr.ru/post/134616/
“L-Systems — математическая красота растений”:http://habrahabr.ru/post/69989/
“FRACTALS – построение геометрических фракталов”:http://flash.xaoc.ru/index.swf
Фракталы - “http://elementy.ru/posters/fractals”:http://elementy.ru/posters/fractals

Программы

Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.

Для запуска всех программ нужен .net Framework версии 3.5 или выше.